
কষে দেখি ১.১
1.নিচের বহুপদী সংখ্যামালা গুলির মধ্যে কোনটি/কোনগুলি দ্বিঘাত বহুপদী সংখ্যা মালা বুঝে লিখি ।
(i) x2-7x+2
সমাধানঃ
এটি একটি দ্বিঘাত বহুপদী সংখ্যামালা কারণ এক্ষেত্রে বহুপদী সংখ্যামালার x এর সর্বোচ্চ ঘাত 2 ।
(ii) 7×5-x(x+2)
সমাধানঃ
7x5-x(x+2)
=7x5-x2-2x
এটি একটি বহুপদী সংখ্যামালা হলেও দ্বিঘাত বহুপদী সংখ্যামালা নয় কারণ এক্ষেত্রে x এর সর্বোচ্চ ঘাত 5
(iii) 2x(x+5)+1
সমাধানঃ
2x(x+5)+1
=2x2+10x+1
এটি একটি দ্বিঘাত বহুপদী সংখ্যামালা কারণ এক্ষেত্রে বহুপদী সংখ্যামালার x এর সর্বোচ্চ ঘাত 2 ।
(iv) 2x-1
সমাধানঃ
এটি দ্বিঘাত বহুপদী সংখ্যামালা নয় কারণ এক্ষেত্রে x এর সর্বোচ্চ ঘাত 2 নয় ।
2.নীচের সমীকরণগুলির কোনটি ax²+bx+c=0,যেখানে a,b,c বাস্তবসংখ্যা এবং a≠0 আকারে লেখা যায় তা লিখি।
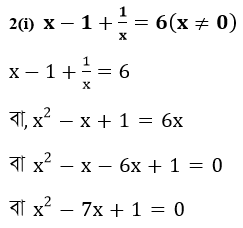
∴ প্রদত্ত সমীকরণটিকে ax2+bx+c আকারে প্রকাশ করা গেল ।
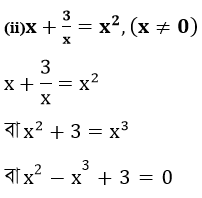
∴ প্রদত্ত সমীকরণটিকে ax2+bx+c আকারে প্রকাশ করা যায় না ।
(iii) x2-6√x+2=0
x2-6√x+2=0
∴ প্রদত্ত সমীকরণটিকে ax2+bx+c আকারে প্রকাশ করা যায় না ।
(iv) (x-2)2 = x2-4x+4
(x-2)2 = x2-4x+4
বা, x2-4x+4 = x2-4x+4
∴ প্রদত্ত সমীকরণটিকে ax2+bx+c আকারে প্রকাশ করা যায় না কারণ এটি একটি অভেদ ।
3. x6-x3-2=0 সমীকরণটি চলের কোন ঘাতের সাপেক্ষে একটি দ্বিঘাত সমীকরণ তা নির্ণয় করি।
সমাধানঃ
x6-x3-2=0
বা, (x3)2-x3-2=0
∴ প্রদত্ত সমীকরণটিকে ax2+bx+c আকারে প্রকাশ করা গেল।
∴প্রদত্ত সমীকরণ টি x3 এর সাপেক্ষে একটি দ্বিঘাত সমীকরণ ।
4(i) (a-2)2+3x+5=0 সমীকরণটি a এর কোন মানের জন্য দ্বিঘাত সমীকরণ হবেনা তা নির্ণয় করি ।
সমাধানঃ প্রদত্ত সমীকরণ টি দ্বিঘাত সমীকরণ হবেনা যদি a-2= 0 হয়
∴ a=2 হলে প্রদত্ত সমীকরণটি দ্বিঘাত সমীকরণ হবে না ।


(iii) 3x2+7x+23 = (x+4)(x+3)+2- কে ax2+bx+c =0 (a≠0) দ্বিঘাত সমীকরনের আকারে প্রকাশ করি ।
সমাধানঃ
3x2+7x+23 = (x+4)(x+3)+2
বা, 3x2+7x+23=x2+4x+3x+12+2
বা, 3x2+7x+23=x2+7x+14
বা, 3x2-x2+7x-7x+23-14=0
বা, 2x2+9=0
বা, 2x2+0x+9=0
∴ প্রদত্ত সমীকরণটিকে ax2+bx+c আকারে প্রকাশ করা গেল যেখানে a≠0 ।
(iv) (x+2)3=x(x2-1) -কে ax2+bx+c=0,(a≠0) দ্বিঘাত সমীকরনের আকারে প্রকাশ করি এবং x2,x ও x0 এর সহগ লিখি।
সমাধানঃ
(x+2)3=x(x2-1)
বা, x3+3x2(2)+3(x)(2)2+(2)3 =x3-x
বা, x3+6x2+12x+8=x3-x
বা, 6x2+13x+8=0
∴ প্রদত্ত সমীকরণটিকে ax2+bx+c আকারে প্রকাশ করা গেল যেখানে a≠0 এবং x² এর সহগ 6 , x এর সহগ 13 এবং x0 এর সহগ 8 ।
5. নিচের বিবৃতি গুলি থেকে একচল বিশিষ্ট দ্বিঘাত সমীকরণ গঠন করি ।
(i) 42 কে দুটি অংশে বিভক্ত করো যাতে একটি অংশ অপর অংশের বর্গের সমান হয়।
সমাধানঃ
ধরি , একটি অংশ x
∴ অপর অংশ (42-x)
শর্তানুসারে,
x2=(42-x)
বা, x²+x-42=0
∴ x²+x-42=0 হল নির্ণেয় দ্বিঘাত সমীকরণ ।
(ii) দুটি ক্রমিক ধনাত্মক অযুগ্ম সংখ্যার গুনফল 143
সমাধান ঃ ধরি একটি সংখ্যা x
∴ অপর সংখ্যাটি হবে (x+2) [ যেহেতু ক্রমিক ধনাত্মক অযুগ্ম সংখ্যা ]
শর্তানুসারে,
X(x+2)=143
বা, x²+2x-143=0
∴ x²+2x-143=0 হল নির্ণেয় দ্বিঘাত সমীকরণ ।
(iii) দুটি ক্রমিক সংখ্যার বর্গের সমষ্টি 313 ।
সমাধানঃ
ধরি , একটি সংখ্যা x
∴ অপর সংখ্যা (x+1)
শর্তানুসারে,
x2+(x+1)2 =313
বা,x²+x²+2x+1=313
বা, 2x²+2x+1=313
বা, 2x²+2x+1-313=0
বা 2x²+2x-312=0
বা, x²+x-156=0 [ উভয়পক্ষে 2 দ্বারা ভাগ করে পাই ]
∴ x²+x-156=0,হল নির্ণেয় দ্বিঘাত সমীকরণ ।
6. নিচের বিবৃতি গুলি থেকে একচল বিশিষ্ট দ্বিঘাত সমীকরণ গঠন করি ।
(i) একটি আয়তকার ক্ষেত্রের কর্ণের দৈর্ঘ্য 15 মিটার এবং তার দৈর্ঘ্য প্রস্থ অপেক্ষা 3মিটার বেশি ।
সমাধানঃ
ধরি , আয়তক্ষেত্রের প্রস্থ x মিটার
∴ আয়তক্ষেত্রের দৈর্ঘ্য (x+3) মিটার
আয়তক্ষেত্রের কর্ণের দৈর্ঘ্য =√(দৈর্ঘ্য²+প্রস্থ²)
শর্তানুসারে ,

উভয়পক্ষ কে বর্গ করে পাই,
x²+(x+3)²=225
বা, x²+x²+2(x)3+(3)²=225
বা, 2x²+6x+9=225
বা, 2x²+6x+9-225=0
বা, 2x²+6x-216=0
বা, x²+3x-108=0 [উভয়পক্ষে 2 দ্বারা ভাগ করে পাই ]
∴ নির্ণেয় দ্বিঘাত সমীকরণটি হল x²+3x-108=0
(ii) এক ব্যাক্তি 80 টাকায়ে কয়েক কিগ্রা চিনি ক্রয় করলেন। যদি ওই টাকায়ে তিনি আর ও 4 কিগ্রা চিনি বেশি পেতেন তবে তার কিগ্রা প্রতি চিনির দাম 1 টাকা কম হত ।
ধরি , প্রতি কিগ্রা চিনির মূল্য x টাকা
∴ 80 টাকায় পাওয়া যাবে 80/x কিগ্রা চিনি
এখন প্রতি কিগ্রা চিনির দাম (x-1)টাকা হলে, 80 টাকায় পাওয়া যাবে 80/(x-1) কিগ্রা চিনি
শর্তানুসারে,

∴ নির্ণেয় দ্বিঘাত সমীকরণটি হল x²-x-20 =0
(iii) দুটি স্টেশন এর মধ্যে দূরত্ব 300 km ।একটি ট্রেন প্রথম স্টেশন থেকে সমবেগে দ্বিতীয় স্টেশন এ গেল । ট্রেন টির গতিবেগ ঘণ্টায়ে 5km বেশি হলে ট্রেন টির দ্বিতীয় স্টেশন এ যেতে 2 ঘণ্টা সময় কম লাগত ।
সমাধানঃ
ধরি , ট্রেন টির গতিবেগ xকিমি/ঘন্টা
∴ 300 কিমি যেতে ট্রেনটির সময় লাগবে 300/x ঘন্টা [ যেহেতু , সময় = দূরত্ব /গতিবেগ]
ট্রেনটির গতিবেগ (x+5) কিমি প্রতি ঘণ্টা হলে, 300 কিমি যেতে সময় লাগবে 300/(x+5) ঘণ্টা [ যেহেতু , সময় = দূরত্ব /গতিবেগ]।
শর্তানুসারে ,

∴ নির্ণেয় দ্বিঘাত সমীকরণটি হল x²+5x-750=0
(iv) একজন ঘড়ি বিক্রেতা একটি ঘড়ি ক্রয় করে 336 টাকায়ে বিক্রি করলেন ।তিনি যত টাকায়ে ঘড়ি টি ক্রয় করেছিলেন শতকরা তত টাকা তার লাভ হল ।
ধরি , ঘড়িটি তিনি x টাকায়ে ক্রয় করেছিলেন ।
এবং ঘড়িটি বিক্রি করেছেন 336 টাকায়ে
∴ লাভ= ক্রয়মূল্য – বিক্রয় মূল্য =(336-x) টাকা
∴ শতকরা লাভ= (লাভ/ক্রয় মূল্য)×100=(336-x)/x × 100 %
শর্তানুসারে ,
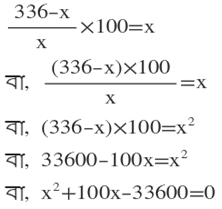
∴ নির্ণেয় দ্বিঘাত সমীকরণটি হল x²+100x-33600=0
(v) স্রোতের বেগ ঘণ্টায়ে 2km হলে রতন মাঝি স্রোতের অনুকুলে 21km গিয়ে ওই দূরত্ব ফিরে আস্তে 10 ঘণ্টা সময় লাগে ।
সমাধানঃ
ধরি, নৌকার বেগ x কিমি /ঘণ্টা
∴স্রোতের অনুকুলে নৌকার বেগ = (x+2) কিমি/ ঘণ্টা
এবং স্রোতের প্রতিকুলে নৌকার বেগ = (x-2) কিমি/ ঘণ্টা
সময় = দুরত্ব/গতিবেগ
∴ স্রোতের অনুকূলে 21 কিমি. যেতে সময় লাগে 21/(x+2) ঘণ্টা এবং স্রোতের প্রতিকূলে 21 কিমি. ফিরে আসতে সময় লাগে 21/(x-2) ঘণ্টা ।
শর্তানুসারে,
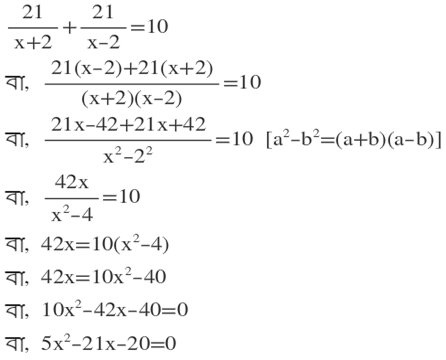
∴ নির্ণেয় দ্বিঘাত সমীকরণটি হল 5x²-21x-20=0
6(vi) আমাদের বারির বাগান পরিষ্কার করতে মহিম অপেহ্মা মজিদের 3 ঘণ্টা বেশি সময় লাগে । তারা উভয় একসঙ্গে কাজটি 2 ঘণ্টায়ে শেষ করতে পারে ।
সমাধানঃ
ধরি, মহিমের বাগান পরিষ্কার করতে সময় লাগে x ঘণ্টা
∴ মজিদের সময় লাগে (x+3) ঘণ্টা
আরও ধরাযাক মোট কাজের পরিমাণ 1 অংশ ।
∴মহিম x ঘণ্টায়ে কাজ করে 1 অংশ
∴ মহিম 1 ঘণ্টায়ে কাজ করে 1/x অংশ
মজিদ (x+3) ঘণ্টায়ে কাজ করে 1 অংশ
∴ মজিদ 1 ঘণ্টায়ে কাজ করে 1/(x+3) অংশ

শর্তানুসারে,
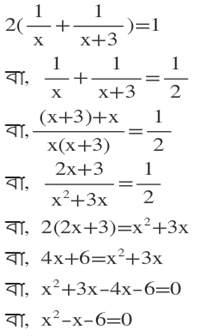
∴ নির্ণেয় দ্বিঘাত সমীকরণটি হল x²-x-6=0
(vii) দুই অঙ্ক বিশিষ্ট একটি সংখ্যার একক স্থানীয় অঙ্ক টি দশক স্থানীয় অঙ্ক অপেহ্মা 6 বেশি এবং অঙ্ক দ্বয়ের গুনফল সংখ্যাটি থেকে 12 কম ।
সমাধানঃ
ধরি দুই অঙ্ক বিশিষ্ট সংখ্যার দশক স্থানীয় অঙ্ক x
∴ একক স্থানীয় অঙ্ক হবে (x+6)
∴ দুই অঙ্ক বিশিষ্ট সংখ্যাটি হল 10x+(x+6)=11x+6
শর্তানুসারে ,
x(x+6)=(11x+6)–12
বা, x²+6x=11x-6
বা, x²+6x-11x+6=0
বা, x²-5x+6=0
∴ নির্ণেয় দ্বিঘাত সমীকরণটি হল x²-5x+6=0
6(viii) 45 মিটার দীর্ঘ ও 40 মিটার প্রসস্থ একটি আয়তক্ষেত্রাকার খেলার মাঠের বাইরের চারপাশে সমান চওড়া একটি রাস্তা আছে এবং ওই রাস্তার ক্ষেত্রফল 450 বর্গ মিটার ।
সমাধান ঃ
ধরি রাস্তাটি x মিটার চওড়া
∴ রাস্তা সহ আয়তক্ষেত্রের দৈর্ঘ্য (45+2x) মিটার
এবং রাস্তা সহ আয়তক্ষেত্রের প্রস্থ (40+2x) মিটার
শর্তানুসারে,
(45+2x)×(40+2x)- (45×40)= 450
বা, 1800+90x+80x+4x² -1800=450
বা, 4x²+170x-450=0
বা, 2x²+85x-225=0
∴ নির্ণেয় দ্বিঘাত সমীকরণটি হল 2x²+85x-225=0 ।
কষে দেখি ১.২
1.নিচের প্রতি ক্ষেত্রে প্রদত্ত মান গুলি দ্বিঘাত সমীকরণের বীজ হবে কিনা যাচাই করে লিখি:
(i) x2+x+1=0 , 1 ও -1
(ii) 8×2+7x=0 , 0 ও -2
(iii) x+1/x=13/6, 5/6 ও 4/3
(iv) x2-√3x-6=0, -√3 ও 2√3
সমাধানঃ
(i) 1 এবং -1 প্রদত্ত সমীকরণ টির বীজ হলে সমীকরণটিকে সিদ্ধ করবে ।
এখন, x2+x+1=0 সমীকরনে x স্থানে 1 এবং -1 বসিয়ে পাই ,
(1)2+1+1 = 1+1+1=3 ≠ 0
আবার, (-1)2+(-1)+1 =1-1+1=1≠ 0
সমীকরণটি 1 এবং -1 কোনোটিই দ্বারা সিদ্ধ নয় সুতরাং 1 এবং -1 প্রদত্ত দ্বিঘাত সমীকরণের বীজ হবে না।
(ii) 0 এবং 2 প্রদত্ত সমীকরণ টির বীজ হলে সমীকরণ টিকে সিদ্ধ করবে ।
এখন, 8x2+7x=0 সমীকরণটিতে x স্থানে 0 এবং 2 বসিয়ে পাই ,
8(0)2+7(0)=0
∴ 0, প্রদত্ত দ্বিঘাত সমীকরণটিকে সিদ্ধ করছে সুতরাং 0 প্রদত্ত দ্বিঘাত সমীকরণের একটি বীজ ।
আবার, 8(2)2+7(2) =32+14=46≠ 0
2 প্রদত্ত দ্বিঘাত সমীকরণটিকে সিদ্ধ করছে না সুতরাং 2 প্রদত্ত দ্বিঘাত সমীকরণের একটি বীজ নয় ।
(iii) 5/6 এবং 4/3 প্রদত্ত দ্বিঘাত সমীকরণটির বীজ হলে সমীকরণটিকে সিদ্ধ করবে ।
এখন, x+1/x=13/6 সমীকরণটিতে x স্থানে 5/6 এবং 4/3 বসিয়ে পাই ,
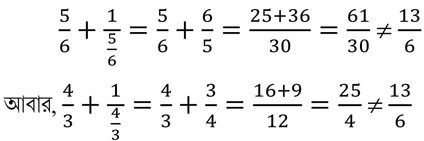
∴ 5/6 এবং 4/3 কোনোটিই প্রদত্ত দ্বিঘাত সমীকরণটির বীজ নয়।
(iv) -√3 এবং 2√3 প্রদত্ত সমীকরণ টির বীজ হলে সমীকরণ টিকে সিদ্ধ করবে ।
এখন, x2-√3x-6=0 সমীকরণটিতে x স্থানে √3 এবং 2√3 বসিয়ে পাই ,
(-√3)2-√3(-√3)-6=3+3-6=6-6=0
∴-√3 প্রদত্ত দ্বিঘাত সমীকরণটিকে সিদ্ধ করছে সুতরাং -√3 প্রদত্ত দ্বিঘাত সমীকরণের একটি বীজ হবে ।
আবার, (2√3)2-√3(2√3)-6=12-6-6=12-12=0
∴2√3 প্রদত্ত দ্বিঘাত সমীকরণটিকে সিদ্ধ করছে সুতরাং 2√3 প্রদত্ত দ্বিঘাত সমীকরণের একটি বীজ হবে ।
2(i) K এর কোন মানের জন্য 7x²+kx-3=0 দ্বিঘাত সমীকরণের একটি বীজ 2/3 হবে ?
সমাধানঃ

∴ K এর মান -1/6 হলে 7x²+kx-3=0 দ্বিঘাত সমীকরণের একটি বীজ 2/3 হবে ।
2(ii)K এর কোন মানের জন্য x² +3ax+k=0 দ্বিঘাত সমীকরণের একটি বীজ হবে –a ?
সমাধানঃ
x² +3ax+k=0 দ্বিঘাত সমীকরণের একটি বীজ –a
∴ -a সমীকরণ টিকে সিদ্ধ করবে
X এরস্থানে –a বসিয়ে পাই ,
(-a)²+3a(-a)+k=0
বা, a²-3a²+k=0
বা,-2a²+k=0
বা, k=2a²
∴ k এর মান 2a² হলে দ্বিঘাত সমীকরণটির একটি বীজ হবে -a ।
3. যদি ax²+7x+b=0 দ্বিঘাত সমীকরণের দুটি বীজ 2/3 এবং -3 হয় তবে a ও b এর মান নির্ণয় করি ।
সমাধান ঃ
যদি ax²+7x+b=0 দ্বিঘাত সমীকরণের দুটি বীজ 2/3 এবং-3 হয় তাহলে 2/3 এবং -3 উভয়ই প্রদত্ত দ্বিঘাত সমীকরণটিকে সিদ্ধ করবে ।
x এর স্থানে 2/3 এবং -3 বসিয়ে পাই ,
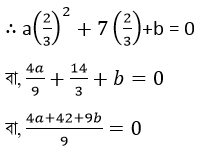
বা, 4a + 9b +42 = 0
বা, 4a+9b = -42
এবং a(-3)² + 7(-3)+b=0
বা, 9a-21+b=0
বা, 9a+b=21—(ii)
(ii) নং সমীকরণ কে 9 দ্বারা গুন করে (i) নং সমীকরণ বিয়োগ করে পাই ,
(4a+9b)-(81a+9b)=-42-189
বা, -77a = -231
বা , a = -231/-77
বা , a = 3
a এর প্রাপ্ত মান (i) নং সমীকরণে বসিয়ে পাই
4(3)+9b=-42
বা, 12+9b = -42
বা, 9b= -42-12
বা, 9b = -54
বা, b= -54/9
বা, b = -6
∴ ax²+7x+b=0 দ্বিঘাত সমীকরণের দুটি বীজ 2/3 এবং-3 হলে, a=3 এবং b= -6 হবে।
4.সমাধান করি:
(i) 3y² -20=160-2y²
3y² -20=160-2y²
বা , 3y²+2y²=160+20
বা, 5y² =180
বা, y² = 180/5
বা, y² =36
বা, y= ±√36
বা, y =± 6
∴ নির্ণেয় সমাধান y=6 এবং y=-6
(ii) (2x+1)² +(x+1)²=6x+47
(2x+1)² +(x+1)²=6x+47
বা, (2x)²+2(2x)1+(1)² + (x)²+2x+(1)²=6x+47
বা, 4x² +4x +1 + x²+2x+1=6x+47
বা, 5x²+6x+2 =6x+47
বা, 5x²+6x+2-6x-47=0
বা, 5x²-45 =0
বা ,5x²=45
বা , x²=45/9
বা, x²=9
বা, x=±√9
বা, x = ±3
∴নির্ণেয় সমাধান x=3 এবং x=-3
(iii) (x-7)(x-9)=195
(x-7)(x-9)=195
বা, x(x-9)-7(x-9)=195
বা, x²-9x-7x+63=195
বা, x²-16x+63-195=0
বা, x²-16x-132=0
বা, x²-(22-6)x-132=0
বা, x²-22x+6x-132=0
বা, x(x-22)+6(x-22)=0
বা, (x-22)(x+6)=0
দুটি রাশির গুনফল শূন্য
হয় (x-22)=0
∴ x=22
অথবা , (x+6)=0
∴ x=-6
∴ নির্ণেয় সমাধান x= 22 এবং x= -6

∴ নির্ণেয় সমাধান x=3 এবং x=-3
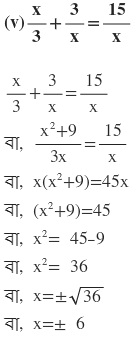
∴ নির্ণেয় সমাধান x=6 এবং x=-6
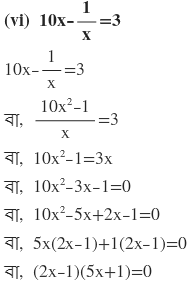
দুটি রাশির গুনফল শূন্য
হয় (2x-1)=0
2x=1
বা, x=1/2
অথবা (5x+1)=0
∴ 5x= -1
বা, x= -1/5
∴ নির্ণেয় সমাধান x=1/2 এবং x= -1/5

দুটি রাশির গুনফল শূন্য
হয় (x-2)=0
∴ x=2
অথবা (2x-1)=0
∴ 2x=1
বা, x= 1/2
∴ নির্ণেয় সমাধান x=2 এবং x=1/2 ।

দুটি রাশির গুনফল শূন্য
হয় x=0
অথবা (3x-2)=0
বা, 3x=2
বা, x=2/3
∴ নির্ণেয় সমাধান x=0 এবং x=2/3

দুটি রাশির গুনফল শূন্য
হয় (x+9)=0
∴ x= -9
অথবা (x-7)=0
∴ x=7
∴ নির্ণেয় সমাধান x=-9 এবং x=7
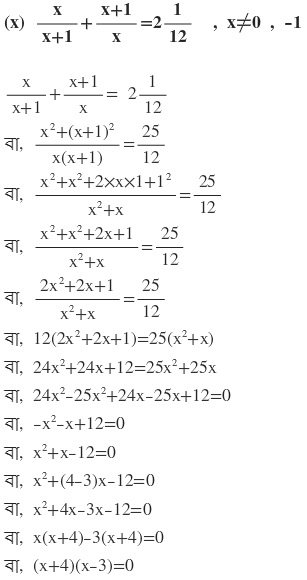
দুটি রাশির গুনফল শূন্য
হয় (x+4)=0
বা, x=-4
অথবা (x-3)=0
বা, x=3
∴ নির্ণেয় সমাধান x=3 এবং x=-4
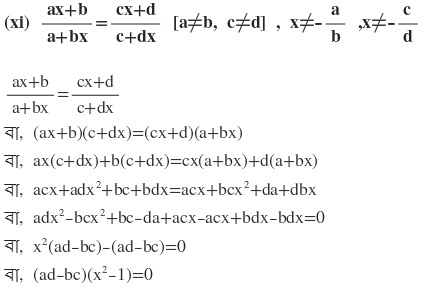
এখন দুটি রাশির গুনফল শূন্য
কিন্তু (ad-bc)≠ 0 কারণ a≠b এবং c≠d
∴ (x² -1)=0
বা , x² =1
বা, x = ±√1
∴ নির্ণেয় সমাধান X= 1 এবং X= -1
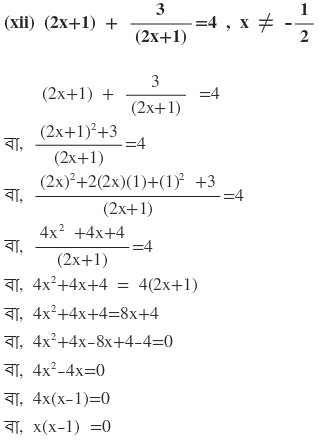
দুটি রাশির গুনফল শূন্য
হয় x=0
অথবা (x-1)=0
বা, x=1
∴ নির্ণেয় সমাধান x=0 এবং x= 1
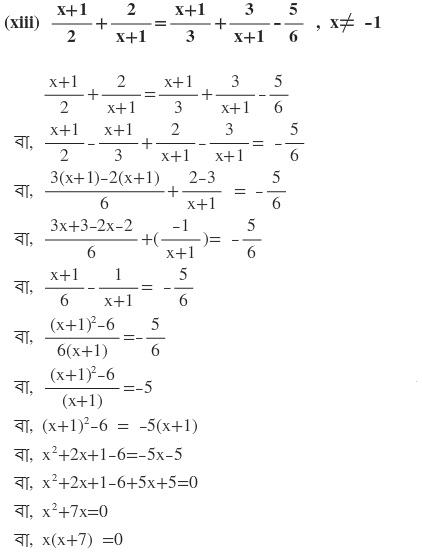
দুটি রাশির গুনফল শূন্য
হয় x=0
অথবা (x+7)=0
বা, x= -7
∴ নির্ণেয় সমাধান x= 0 এবং x=-7 ।

দুটি রাশির গুনফল শূন্য
হয়, (9x+68)=0
বা, 9x=-68
বা, x=-68/9
অথবা, (x-3)=0
বা, x=3
∴ নির্ণেয় সমাধান x=3 এবং x= -68/9

দুটি রাশির গুনফল শূন্য
হয় (a-3)=0
বা, a=3
অথবা, (a-2)=0
বা, a=2

∴ নির্ণেয় সমাধান x=6 এবং x= 9 ।

দুটি রাশির গুনফল শূন্য
হয়, (x+a)=0
বা, x= -a
অথবা, (x+b)=0
বা, x= -b
∴ নির্ণেয় সমাধান x=-a এবং x=-b

দুটি রাশির গুনফল শূন্য
হয় (m-3)=0
বা, m=3
অথবা (m-2)=0
বা, m=2


দুটি রাশির গুনফল শূন্য
হয় (x-a)=0
বা, x=a
অথবা (x+a+b)=0
বা, x=-(a+b)
∴ নির্ণেয় সমাধান x=a এবং x=-(a+b)

দুটি রাশির গুনফল শূন্য
হয় (x-7)=0
বা, x=7
অথবা (x+2)=0
বা, x=-2
∴ নির্ণেয় সমাধান x= 7 এবং x=-2

দুটি রাশির গুনফল শূন্য
হয় x=0
অথবা![]()
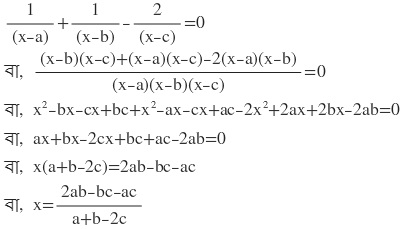
∴ নির্ণেয় সমাধান x=0 এবং x=(2ab-bc-ac)/(a+b-2c)
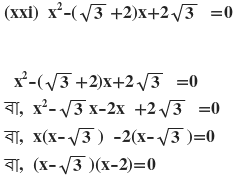
দুটি রাশির গুনফল শূন্য
হয়

∴ নির্ণেয় সমাধান
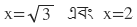
![]()