Source: Internet

Solid State
From earlier studies, we know that liquids and gases are called fluids because of their ability to flow. The fluidity in both of these states is due to the fact that the molecules are free to move about. On the contrary, the constituent particles in solids have fixed positions and can only oscillate about their mean positions.
This explains the rigidity in solids. These properties depend upon the nature of constituent particles and the binding forces operating between them. The correlation between structure and properties helps in the discovery of new solid materials with desired properties.
Objectives
By studying this chapter, you will be able to
• describe general characteristics of solid state;
• distinguish between amorphous and crystalline solids;
• classify crystalline solids on the basis of the nature of binding forces;
• define crystal lattice and unit cell;
• explain close packing of particles;
• describe different types of voids and close packed structures;
• calculate the packing efficiency of different types of cubic unit cells;
• correlate the density of a substance with its unit cell properties;
• describe the imperfections in solids and their effect on properties;
• correlate the electrical and magnetic properties of solids and their structure.
Q 01: Why are solids rigid?
Answer :
Solids have good intermolecular force of attraction, which tend to keep molecules of solid closer. And thus make solid rigid.
Q 02: Why do solids have a definite volume?
Answer :
At room temperature, intermolecular forces bring molecules so close that they cling to one another and occupy fixed positions. They oscillate about their mean position but they have fixed volume. So, due to the fixed position of particles and strong intermolecular force, solids have a definite volume.
Q 03: Why is glass considered a super cooled liquid?
Answer:
Glass is an amorphous solid. Just like liquids, amorphous solids also have a tendency to flow, though very slowly. Therefore, these are called pseudo solids or super cooled liquids.
Q 04: Refractive index of a solid is observed to have the same value along all directions.
Comment on the nature of this solid. Would it show cleavage property ?
Answer :
We know that amorphous solid are isotropic in nature i.e., their properties are same in all directions. According to given description, the nature of given solid is amorphous.
Cleavage property :- When we cut the solid with a sharp edged tool, they cut into two pieces with irregular surfaces.
Q 05: Solid A is a very hard electrical insulator in solid as well as in molten state and melts at extremely high temperature.
What type of solid is it?
Answer :
As per the given properties, Solid A shows the absence of ionic properties in it.
A is a covalent or network solid (exception graphite, which is soft and conductor of electricity).
Q 06: Ionic solids conduct electricity in molten state but not in solid-state. Explain.
Answer :
In the solid state, the ions are not free to move about so they are electrical insulators. But, in the molten state or when ionic solids are dissolved in water, the ions become free to move about so they conduct electricity.
Q 07: What type of solids are electrical conductors, malleable and ductile?
Answer :
Metallic solids are hard but malleable and ductile. Also, they are conductors in solid as well as in the molten state.
Q 08: Give the significance of a ‘lattice point’.
Answer :
A crystal lattice is the pattern of points representing the locations of motifs. And each point in a lattice is called lattice points. These points are significant as they represent one constituent particle which may be an atom, a molecule (a group of atoms) or an ion.
Q 09: Name the parameters that characterise a unit cell.
Answer :
A unit cell is characterised by:-
(i) its dimensions along the three edges a, b and c. These edges may or may not be mutually perpendicular.
(ii) angles between the edges, α (between b and c), β (between a and c) and γ (between a and b). Thus, a unit cell is characterised by six parameters
a, b, c, α, β and γ.
Q 10: Distinguish between
(i) Hexagonal and monoclinic unit cells
(ii) Face-centred and end-centred unit cells
Answer :(i) Hexagonal and monoclinic unit cells:-
| Properties | Hexagonal | Monoclinic |
| Possible Variation | Primitive | Primitive, End centered |
| Axial distance | ||
| Axial angles | ||
| Examples | Graphite, ZnO | Monoclinic sulphur |
(ii) Face-centred and end-centred unit cells: –
- A face-centred unit cell contains atoms at all the corners and at the centre of all the faces, whereas in end – centred unit cell one pair of opposite faces contains atoms apart from atoms at all the corners.
- The total number of atoms in a unit cell differs by 1.
Q 11: Explain how much portion of an atom located at
(i) corner and
(ii) body centre of a cubic unit cell is part of its neighbouring unit cell.
Answer :
(i) At corner:- Each atom at a corner is shared between eight adjacent unit cells, four unit cells in the same layer and four unit cells of the upper (or lower) layer. Therefore, only of an atom (or molecule or ion) actually belongs to a particular unit cell.
(ii) At body centre of cubic cell :- Since body centre atom completely belongs to the unit cell in which it is present, thus it is not part of any neighbouring unit cell. So, one atom belongs to a one unit cell.
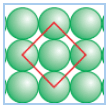
Q 12: What is the two dimensional coordination number of a molecule in square close-packed layer?
Answer :
In two dimensional square closed packed layer, one atom is in contact with 4 of its neighbouring atoms. So its coordination number is 4.

Q 13: A compound forms hexagonal close-packed structure. What is the total number of voids in 0.5 mol of it? How many of these are tetrahedral voids?
Answer :
We know amount of compound given = 0.5 mol,
So, No. of atoms
We also know that, No. of tetrahedral voids = 2 (No. of atoms in closed packing)
No. of octahedral voids = No. of atoms present in closed packing.
So, Total number of voids = No. of tetrahedral voids + No. of octahedral voids.
Q 14: A compound is formed by two elements M and N . The element N forms ccp and atoms of M occupy 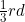 of tetrahedral voids.
of tetrahedral voids.
What is the formula of the compound?
Answer :
It is given that element N forms CCP.
Let us assume, the number of atoms of element N (which forms ccp) is x.
Then no. of tetrahedral voids = 2x.
It is also given that M occupies of tetrahedral voids.
So the number of atoms of element M :
So the molecular formula becomes : 2
3 .
Q 15: An element with molar mass 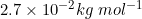 forms a cubic unit cell with edge length
forms a cubic unit cell with edge length 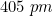 . If its density is
. If its density is 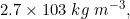 what is the nature of the cubic unit cell?
what is the nature of the cubic unit cell?
Answer :
We know that :
We are given : and
and
So we need to find z (no. of atoms present in unit cell) by putting all values in formula of density.
We get, .
It is known that face centred cubic also has 4 atoms in its unit cell, So given cubic unit cell is face centred.
Q 16: What type of defect can arise when a solid is heated? Which physical property is affected by it and in what way?
When a solid is heated some of the atoms moves out due to increase in its thermal energy. This leads to a vacancy defect. Affected physical property:- Since some of the atoms moved out so its density decreases.
Q 17: What type of stoichiometric defect is shown by  ?
?
ZnS shows Frenkel defect because there is a large difference in the size of Zn and S.
Q 18: Explain how vacancies are introduced in an ionic solid when a cation of higher valence is added as an impurity in it.
Answer :
In impurity defect, the higher valency cation replaces the lower valency cation. An important point to be noted is that electrical neutrality is maintained.
For e.g. In case of NaCl and SrCl2 , some of the sites of Na+ ions are occupied by Sr2+ . Two Na+ ions are replaced by Sr+2 ions. It occupies the site of one ion and the other site remains vacant. The cationic vacancies thus produced are equal in number to that of Sr2+ ions.
Q 19: How can you determine the atomic mass of an unknown metal if you know its density and the dimension of its unit cell? Explain.
Answer :
We know that density is related to molar mass and edge length by the formula :
where
d= Density
a3 = The volume of the unit cell
M= Atomic mass
Z = No. of atoms in unit cell
Na = Avogadro’s number.
Q 20: How will you distinguish between the following pairs of terms:
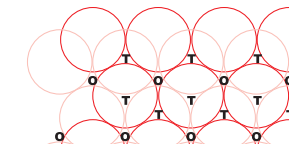
Tetrahedral void and octahedral void
Answer :
Tetrahedral void:- When a sphere (atom) of the second layer is above the void of the first layer (or vice versa) production of a tetrahedral void takes place. These voids are known as tetrahedral voids as, when the centres of these four spheres are joined a tetrahedron is formed.
Octahedral void:- The voids having a triangular in shape (or triangular voids) in the second layer are above the triangular voids in the first layer, also the triangular shapes of these do not overlap. One of them has the apex of the triangle pointing upwards and the other downwards. These voids are surrounded by six spheres/atoms and called as octahedral voids.
Q 21: Calculate the efficiency of packing in case of a metal crystal for simple cubic
Answer:
Simple cubic :- In a simple cubic lattice the atoms are located only on the corners of the cube.
Thus, the side of the cube ‘a’, and the radius of each particle, r are related as: a = 2r
Volume of cubic unit cell = =
And Volume of 1 atom :
Thus packing efficiency of simple cubic is
Q 22: Calculate the efficiency of packing in case of a metal crystal for body-centred cubic
Answer:
Body centred cubic:- In body centred cubic, we have atoms at all corners and at body centre.
Clearly, the atom at the centre will be in touch with the other two atoms diagonally arranged. ; and
Also the length of body diagonal is equal to 4r.
Thus,
The volume of a cube :
In BCC, the total number of atoms is 2.
Q 23: Silver crystallises in fcc lattice. If edge length of the cell is 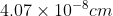 and density is
and density is  , calculate the atomic mass of silver.
, calculate the atomic mass of silver.
Answer :
The relation between density, molar mass and edge length is given by:-
It is given that silver crystallises in fcc lattice, so the value of z = 4. (since it is known that 4 atoms are completely efficient in fcc lattice)
Convert these into SI units,
Q 24: Niobium crystallises in body-centred cubic structure. If density is 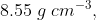 , calculate atomic radius of niobium using its atomic mass
, calculate atomic radius of niobium using its atomic mass 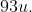
Answer :
Here we will use the relation between density and edge length.
It is given that Niobium crystallises in body-centred cubic structure so the value of z = 2.
So we will put the value of density, molar mass and z.
We get
or or
We know the relation between the radius of the atom and edge length in bcc lattice.
we get the radius of niobium atom = 143.1 pm.
Q 25: If the radius of the octahedral void is r and radius of the atoms in close packing is R , derive relation between r and R.
Answer:
From the below figure it is clear that we can use Pythagoras theorem and find the relation between R and r.
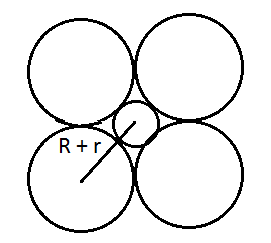
Using pythagoreas theorem :
or
or
or
Q 26: Analysis shows that nickel oxide has the formula  . What fractions of nickel exist as
. What fractions of nickel exist as 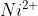 and
and 
Answer :
Given formula is Ni0.98 O1.00 .
Ratio of Ni to O is 0.98.
This means 98 Ni are required for 100 atoms of O.
Let us assume that Ni+2 ions are x.
So the number of Ni+3 ions will be 98 – x.
Using the charge neutrality principle, the net charge of Ni should be equal to a net charge of O.
So the equation becomes : x(2) + (98-x)3 = 2(100)or 2x + 294 – 3x = 200or x = 94.
Thus the fraction of Ni+2 ions =
and fraction of Ni+3 ions = 4%
fraction of Ni+2 ions = 100 – 4 = 96%
Q 27: Aluminium crystallises in a cubic close-packed structure. Its metallic radius is 125 pm.
How many unit cells are there in 1.00 cm3 of aluminium?
Answer :
For cubic close-packed structure,
we have
Given :
the volume of one unit cell
Total unit cells in 1.00 cm3
![]()