SOURCE: Theoretical Content from Internet & Video Content from সমগ্র শিক্ষা মিসন (পূর্ব মেদিনীপুর)

Units & Dimensions – একক ও মাত্রা
একক (Units) কি ?
যে আদর্শ পরিমাণের সাথে তুলনা করে কোনো ভৌত রাশিকে পরিমাপ করা হয় তাকে, পরিমাপের একক বলা হয়।
মাত্রা (Dimensions) কি ?
কোনো ভৌত রাশিতে উপস্থিত মৌলিক রাশিগুলোর সূচককে রাশিটির মাত্রা বলে।
মাত্রা সমীকরণ
মাত্রা সমীকরণ হলো এমন গাণিতিক সমীকরণ, যার সহায়তায় কোনো গাণিতিক রাশির মাত্রা প্রকাশ করা যায়। কোন ভৌত রাশিতে উপস্থিত মৌলিক রাশিগুলোর সূচককে ঐ রাশিটির মাত্রা বলে। আর যে সমীকরণের সাহায্যে কোন রাশির মাত্রা প্রকাশ করা হয়ে থাকে তাকে মাত্রা সমীকরণ বলে।
রাশির প্রেক্ষিতে মাত্রা সমীকরণ এরকম হতে পারে:
- বল, [F] = [MLT−2]
- কাজ, [W] = [ML2T−2]
- ক্ষমতা, [p] = [ML2T−3]
- শক্তি, [E] = [ML2T−2]
- ঘনত্ব, [ρ] = [ML−3]
- চাপ, [p] = [ML−1T−2]
- তাপ, [Q] = [ML2T−2]
- তাপ ধারণ ক্ষমতা, [C] = [ML2T−2θ−1]
কোনো ভৌতরাশিতে (Physical quantities) মূল রাশিগুলি কীভাবে উপস্থিত থাকে তা ওই রাশির মাত্রা (Dimensions) নির্ধারণ করে ।
সংজ্ঞা : কোনো ভৌতরাশিতে (Physical quantities) গুণ বা ভাগের মাধ্যমে উপস্থিত বিভিন্ন মৌলিক রাশিগুলির চিহ্নের উপযুক্ত ঘাত সমন্বিত সাংকেতিক রাশিমালাকে ওই ভৌতরাশির মাত্রা (Dimensions) বলে ।
সকল ভৌতরাশির মাত্রা সাধারণত দৈর্ঘ্যের চিহ্ন [L], ভরের চিহ্ন [M] এবং সময়ের চিহ্ন [T] দ্বারা প্রকাশ করা হয় । [ভৌতরাশি] বললে ওই ভৌতরাশির মাত্রা বোঝায় ।
মাত্রীয় সংকেত : মাত্রার সাহায্যে কোনো ভৌতরাশিকে প্রকাশ করলে তাকে ওই ভৌতরাশির মাত্রীয় সংকেত বলে ।
কয়েকটি ভৌতরাশির মাত্রীয় সংকেত (Dimensional Formulae of some physical quantities) :
(i) [ক্ষেত্রফল] = [দৈর্ঘ্য] x [প্রস্থ] = [দৈর্ঘ্য2 ] = [L2]
Area = [L] × [L] = [L2]
(ii) [আয়তন] = [দৈর্ঘ্য3] = [L3]
Volume = length × length × length = [L3]
(iii) [ঘনত্ব] = [ভর] / [আয়তন] = [M][L3]=[ML−3]
Density = mass volume = ML3 = [L3]
(iv) [বেগ] = [সরণ] / [সময়] = [L][T] = [LT−1]u = ?
Velocity = distance time = [L][T] = [LT^-1]
(v) [ত্বরণ] = [বেগ] / [সময়] = [LT−1][T] = [LT−2]
Acceleration = velocity time = [LT−1][T] = [LT−2]
(vi) [ভরবেগ] = [ভর] x [বেগ] = [M] x [LT-1] = [MLT-1]
(vii) [বল] = [ভর] x [ত্বরণ] = [M] x [LT-2] = [MLT-2]
Force = mass × acceleration = [M][L][T−2] = [MLT−2]
(viii) [কার্য] = [বল] x [সরণ] = [MLT-2] x [L] = [ML2T-2]
Work = Force × distance = [MLT−2] × [L] = [ML2T−2]
(ix) [ক্ষমতা] = [কার্য] / [সময়] = $[ML2T−2][T] = [ML2T−3]
Power = worktime = [ML2T−2][T] = [ML2T−3]
(x) [চাপ] = [বল] / [ক্ষেত্রফল] = [MLT−2][L2] = [ML−1T−2]
Pressure = Force area = [MLT−2][L2] = [ML−1T−2]
কোনো ভৌতরাশির মাত্রীয় সংকেত জানা থাকলে সহজেই রাশিটির একক লেখা সম্ভব । যেমন, আয়তনের মাত্রীয় সংকেত [L3] হওয়ায় এর SI একক মিটার3 (m3) বা ঘনমিটার । অনুরূপে বেগের মাত্রীয় সংকেত [LT-1] হওয়ায় এর SI একক মিটার/সেকেন্ড (ms-1) ।
এককহীন ভৌতরাশির মাত্রা থাকে না । এদের মাত্রীয় সংকেতকে [M0L0T0] এরূপ লেখা যায় । তবে বিশেষ ক্ষেত্রে মাত্রা ছাড়াও একক থাকতে পারে । যেমন রেডিয়ান এককে প্রকাশিত কোণের মাত্রা নেই ।
SOURCE: https://bn.wikipedia.org/wiki/মাত্রা_সমীকরণ
VIDEO CONTENT (PART 1)
সরণ, দ্রুতি ও বেগ
কোনো বস্তু বা বিন্দু একটি অবস্থান থেকে আরেকটি অবস্থানে স্থানান্তরিত হলে, প্রথম অবস্থান থেকে দ্বিতীয় অবস্থান অবধি ভেক্টরকে সরণ বলে।
সরণের পরিমাণ হলো দুটি অবস্থানের মধ্যবর্তী ন্যূনতম দূরত্ব, অর্থাৎ সরলরৈখিক দূরত্ব এবং সরণের দিক প্রথম অবস্থানটি থেকে দ্বিতীয় অবস্থানটির দিকে। যদি বস্তুটি সর্পিল গতিতে প্রথম অবস্থান থেকে দ্বিতীয় অবস্থানে যায়, তাহলে অতিক্রান্ত দূরত্ব সরণের থেকে দৈর্ঘ্যে বেশি। সরণকে s দ্বারা প্রকাশ করা হয়। (s, জার্মান শব্দ “Strecke” এর প্রথম letter থেকে নেয়া হয়েছে । )
সরণ একটি ভেক্টর রাশি। তাই ভেক্টর যোগের নীতি মেনে দুটি সরণকে যোগ করা যায়। অর্থাৎ বিন্দু A থেকে বিন্দু Bতে প্রথম সরণ a ও বিন্দু B থেকে C-তে দ্বিতীয় সরণ b হলে, মোট সরণ বিন্দু A থেকে বিন্দু C-তে সরণের সমতুল্য হবে এবং প্রথমে b ও পরে a পরিমাণ সরণ হলেও মোট সরণ একই হত।
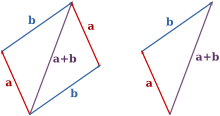
ভেক্টর যোগ
SOURCE: https://bn.wikipedia.org/wiki/সরণ
সরণের একক
এস আই পদ্ধতি ও এম কে এস পদ্ধতিতে সরণের একক হল মিটার।
সিজিএস পদ্ধতিতে সরণের একক হল সেন্টিমিটার।
এপিএস পদ্ধতিতে সরণের একক ফুট।
সরণ ও দূরত্বের মধ্যে পার্থক্য
আপাতদৃষ্টিতে স্মরণ এবং দূরত্বের মধ্যে পার্থক্য কিছু মনে না হলেও বাস্তবে সরণ ও দূরত্বের মধ্যে পার্থক্য অনেক।
১. কোন বস্তু নির্দিষ্ট অভিমুখে স্থান পরিবর্তন করলে কণাটির প্রথম এবং শেষ অবস্থান একটি সরলরেখা দিয়ে যোগ করে যে দূরত্ব পাওয়া যায় তাকে সরণ বলে। আর বস্তুকণার প্রথম এবং শেষ অবস্থান পরিবর্তনে মোট যতটা পথ অতিক্রম করতে হয় সেই পথকে বস্তুটির দ্বারা অতিক্রান্ত দূরত্ব বলে।
২. সরণ একটি ভেক্টর রাশি কিন্তু দূরত্ব হলো একটি স্কেলার রাশি।
সরণ একটি ভেক্টর রাশি ।
দ্রুতি
দ্রুতি কাকে বলে
ক) কোন গতিশীল বস্তু সরল বা বক্র পথে একক সময়ে যে দূরত্ব অতিক্রম করে তাকে ঐ বস্তুর দ্রুতি বলে।
দ্রুতি একটি স্কেলার রাশি। দ্রুতির শুধুমাত্র মান আছে কিন্তু কোন অভিমুখ নেই তাই একে স্কেলার রাশি বলা হয়।
একটি গাড়ি ঘণ্টায় ৬০ কিলোমিটার যায়। এটাই হলো গাড়িটির দ্রুতি। গাড়িটি কোন দিকে যাচ্ছে তা বলার প্রয়োজন হয় না।
কোন বস্তু t সেকেন্ড s দূরত্ব অতিক্রম করে তাহলে বস্তুটির দ্রুতি হবে এক সেকেন্ডে s/t দুরত্ব।
দ্রুতির পরিমাপ = s/t
অর্থাৎ বস্তুর দূরত্ব সমান = (অতিক্রান্ত দূরত্ব / সময়)
দ্রুতির একক
এস আই ও এম কে এস পদ্ধতিতে দ্রুতির একক মিটার/সেকেন্ড
সিজিএস পদ্ধতিতে দ্রুতির একক সেন্টিমিটার/সেকেন্ড
এপিএস পদ্ধতিতে দ্রুতির একক ফুট/সেকেন্ড।
উদাহরণ
মনে করি একটি ট্রেন 3 ঘন্টায় 240 কিলোমিটার পথ অতিক্রম করেছে। তবে ট্রেনটির দ্রুতি হবে 240/3 কিমি/ঘন্টা বা, 80 কিমি/ঘন্টা।
দ্রুতির প্রকারভেদ
দ্রুতির দুই প্রকারের হয়ে থাকে।
১. সমদ্রুতি
২. অসম দ্রুতি
সমদ্রুতি
যদি কোন বস্তু সমান সময়ের ব্যবধানে সর্বদা সমান দূরত্ব অতিক্রম করে তখন, ঐ বস্তুটির গতিকে সমদ্রুতি বলে।
উদাহরণস্বরূপ বলা যেতে পারে বৃত্তাকার পথে ঘূর্ণায়মান কোন বস্তু যদি নির্দিষ্ট সময়ে নির্দিষ্ট দৈর্ঘ্যের চাপকে অতিক্রম করে চলতে থাকে তবে বস্তুটিকে সমদ্রুতি সম্পন্ন বলা হবে। যেমন ঘূর্ণায়মান পাখার ব্লেড।
অসম দ্রুতি
যদি কোন বস্তু সমান সময়ের অবকাশে বিভিন্ন দূরত্ব অতিক্রম করে, তবে বস্তুটির গতিকে অসম দ্রুতি বলে।
অসম দ্রুতির ক্ষেত্রে গড় দ্রুতি নির্ণয় করার প্রয়োজন হয়। অসম দ্রুতির সম্পন্ন কোন বস্তু দ্বারা অতিক্রান্ত দূরত্ব সময় দ্বারা ভাগ করলে বস্তুটির গড় দ্রুতি পাওয়া যায়।
অর্থাৎ বস্তুর গড় দ্রুতি = (অতিক্রান্ত দূরত্ব/মোট সময়)।
মনে করে একটি বাইসাইকেল প্রথম ঘণ্টায় 5 কিলোমিটার দ্বিতীয় ঘন্টায় 7 কিলোমিটার এবং তৃতীয় ঘন্টায় 3 কিলোমিটার গেল। এক্ষেত্রে মোট অতিক্রান্ত দূরত্ব = (5+7+3) = 15 কিলোমিটার এবং মোট সময় = তিন ঘন্টা
সুতরাং, সূত্র অনুসারে বস্তুর গড় দূরত্ব = 15/3 বা, 5 কিলোমিটার/ঘন্টা
পক্ষান্তরে বস্তুর গড় দ্রুতি এবং নির্দিষ্ট দূরত্ব অতিক্রমের জন্য ব্যয়িত সময় জানা থাকলে নির্দিষ্ট দূরত্বটা সহজেই নির্ণয় করা যায়। কারণ মোট অতিক্রান্ত দূরত্ব = গড় দ্রুতি * সময়
বেগ
বেগ কাকে বলে
কোন গতিশীল বস্তুর সরণের পরিবর্তনের হারকে বেগ বলে। অর্থাৎ একক সময়ে কোন বস্তুর নির্দিষ্ট দিকে যে দূরত্ব অতিক্রম করে তাই ঐ বস্তুর বেগ।
সরণ নির্দেশ করার জন্য মানবিক এর প্রয়োজন হয়, কাজেই বেগ নির্দেশের জন্য মান ও দিকের প্রয়োজন হয় । তাই বেগ একটি ভেক্টর রাশি।
যদি t সময়ে কোন বস্তুর সরণ S হয় এবং বেগ V হয় তবে,
বস্তুর গতি বেগ = (বস্তুর সরণ/সময়)
বা, V = S / t
বা, S = V x t
অর্থাৎ বস্তুর সরণ = বস্তুর বেগ x সময়।
বেগের একক
সিজিএস পদ্ধতিতে বেগের একক সেন্টিমিটার/সেকেন্ড।
এসআই এবং এমকেএস পদ্ধতিতে বেগের একক মিটার/সেকেন্ড।
এপিএস পদ্ধতিতে বেগের একক ফুট/সেকেন্ড
অর্থাৎ দ্রুতি ও বেগকে একই এককের সাহায্যে প্রকাশ করা হয়।
বেগের প্রকারভেদ
বস্তুর বেগ দুই প্রকারের হয়ে থাকে
১. সমবেগ
২. অসম বেগ
সমবেগ
কোন বস্তুর বেগের মান ও দিক সব সময় অপরিবর্তিত থাকলে বস্তুটির বেগকে সমবেগ বলে।
কোন বস্তুর বেগ বলতে আমরা বস্তুর সমবেগকে বুঝে থাকি। যেমন কোন বস্তু ২০ মিটার/সেকেন্ড বেগে সরলরেখা বরাবর চললে বস্তুর এই বেগকে আমরা সমবেগ বলি। এক্ষেত্রে বস্তুর বেগের মান এবং দিক সবসময় স্থির থাকে।
অসম বেগ
যদি কোন বস্তুর বেগের মান কিংবা অভিমুখ সময়ের সঙ্গে পরিবর্তিত হয় তবে বস্তুটির বেগকে আমরা অসমবেগ বলি।
যেমন স্থির অবস্থান থেকে যাত্রা শুরু করে কোন বস্তু যদি একই দিকে নির্দিষ্ট ত্বরণে চলে তবে সময়ের সাপেক্ষে ঐ বস্তুর বেগ ক্রমশ বাড়ে ফলে বস্তুটি অসম বেগে চলতে থাকে।
দ্রুতি এবং বেগের মধ্যে পার্থক্য
দ্রুতি এবং বেগ আপেক্ষিকভাবে একই রকম মনে হলেও এদের মধ্যে পার্থক্য বিস্তর।
| দ্রুতি | বেগ |
| কোন বস্তু একক সময়ে যে দূরত্ব অতিক্রম করে তাকে বস্তুর দ্রুতি বলে। | একক সময়ে বস্তুর সরণ কে বস্তুটির বেগ বলে। |
| দ্রুতির মান আছে কিন্তু অভিমুখ নেই তাই দ্রুত একটি স্কেলার রাশি। | কোন বস্তুর বেগ বলার সময় তার মান দিক দুইই নির্দেশ করতে হয় সেজন্য বেগ একটি ভেক্টর রাশি। |
| কোন বস্তুর সমদ্রুতি সম্পন্ন হলেও সমবেগ সম্পন্ন নাও হতে পারে। কারণ বস্তুটি যদি বৃত্তাকার পথে সমদ্রুতিতে চলে তবে ঐ বস্তুর অভিমুখের পরিবর্তন হয় ফলে বস্তুটিকে সমবেগ সম্পন্ন বলা যায় না। | কোন বস্তু সমাবেশ সম্পন্ন হলে তা সমদ্রুতি সম্পন্ন হবে। কারণ দিক অপরিবর্তিত রেখে সমান সমান সমান দূরত্ব অতিক্রম করা কে সমবেগ বলে। আর সমান সময়ে সমান দূরত্ব অতিক্রম করাকে সমদ্রুতি বলে। |
| কোন গতিশীল বস্তুর দ্রুতির মান কখনো শূন্য হতে পারে না | গতিশীল বস্তুর বেগের মান শূন্য হতে পারে। |
| মানের পরিবর্তন হলে দ্রুতিরও পরিবর্তন হয়। | মান বা দিক উভয়ের পরিবর্তন হলে বেগের পরিবর্তন হয়। |
| দ্রুতির ইংরাজি প্রতিশব্দ Speed | বেগের ইংরাজি প্রতিশব্দ Velocity |
প্রশ্নোত্তর
সরণকে ভেক্টর রাশি বলা হয় কেন
সরণ কে নির্দেশ করতে হলে এর মান দিক দুটোকেই নির্দেশ করতে হয়। সরণের মান ও অভিমুখ দুইই আছে । তাই স্মরণ একটি ভেক্টর রাশি। সরনকে দৈর্ঘ্যের এককে প্রকাশ করা হয়।
কোন বস্তু দ্বারা অতিক্রান্ত দূরত্ব শূন্য নয়, কিন্তু ও সরণের মান শূন্য হতে পারে কি?
হ্যাঁ ক্ষেত্রবিশেষে কোন গতিশীল বস্তু ত্বরণের মান শূন্য হতে পারে। ধরি একটি গতিশীল বস্তু সরল রৈখিক পথে A থেকে Bতে এবং B থেকে আবার Aতে ফিরে এলো অতএব সরণ শূন্য হবে। যদিও বস্তুর অতিক্রান্ত দূরত্ব 2AB।
অন্যভাবে কোন গতিশীল বস্তু যদি বৃত্তাকার পথে নির্দিষ্ট দূরত্ব অতিক্রম করে এসে পূর্বের স্থানে থেমে যায় তাহলেও তার সরণ শূন্য হবে।
সুতরাং গতিশীল কোন বস্তুর নির্দিষ্ট দূরত্ব অতিক্রম করলেও বস্তুর সরণ শূন্য হতে পারে।
সমদ্রুতি সম্পন্ন কোন বস্তু কি সব সময় সমবেগ সম্পন্ন হবে
যদি কোন বস্তু আঁকাবাঁকা পথে সামান্য সময়ের ব্যবধানে একই দূরত্ব অতিক্রম করে চলতে থাকে তবে বলা যায় যে বস্তুটি সমদ্রুতিতে চলছে। আঁকাবাঁকা পথ চলার সময় বস্তুটির গতিমুখের পরিবর্তন ঘটে। ফলে ওই বস্তুটিকে সমবেগসম্পন্ন বলা যায় না। কারণ বেগের একটি নির্দিষ্ট অভিমুখ থাকে।
ধরা যাক একটি খেলনা গাড়ি বৃত্তাকার পথে সমদ্রুতিতে চলছে। বৃত্তাকার পথে চলার ফলে গাড়িটির গতির অভিমুখে ক্রমাগত পরিবর্তন ঘটবে। অর্থাৎ বৃত্তাকার পথে গাড়িটির গতির অভিমুখে একই না থাকায় বাড়িতেই সমবেগ সম্পন্ন বলা যাবে না। কিন্তু যদি কোন বস্তুর নির্দিষ্ট অভিমুখে সমদ্রুতিতে চলতে থাকে তবে ওই বস্তুটির সমবেগ সম্পন্ন হবে ।
ত্বরণ ও মন্দন
ত্বরণ কাকে বলে ?
কোনো বস্তুর বেগ যদি ক্রমশ বাড়তে থাকে , তবে সেই বস্তুর বেগের পরিবর্তনের হারকে ত্বরণ বলা হয় । অর্থাৎ একক সময়ে বেগের বৃদ্ধিকেই ত্বরণ বলা হয় ।
ত্বরণ = অতিক্রান্ত দূরত্ব / সময় ।
নির্দিষ্ট ত্বরণে গতিশীল কোন বস্তুর প্রারম্ভিক বেগ u এবং t সময় পরে চূড়ান্ত বেগ v হলে ঐ বস্তুর ত্বরণ f = বস্তুর বেগ বৃদ্ধি/অতিক্রান্ত সময়।
অর্থাৎ বস্তুর ত্বরণ, f = (v-u) / t
ত্বরণের একক কি ?
১) ত্বরণের S.I একক – মিটার প্রতি বর্গ সেকেন্ড (m s−2)
২) ত্বরণের C.G.S একক – সেন্টিমিটার প্রতি বর্গ সেকেন্ড (cm s−2)
৩) FPS পদ্ধতিতে ত্বরণের একক – ফুট/ সেকেন্ড²
৪) এম কে এস পদ্ধতিতে ত্বরণের একক মিটার/সেকেন্ড²
৫) ত্বরণের মাত্রা – L/T
তাৎক্ষণিক ত্বরণ কাকে বলে ?
কোনো মুহূর্তকে ঘিরে অতি অল্প সময় ব্যবধান সময়ের সাপেক্ষে বস্তুর বেগের পরিবর্তনের হারকে তাৎক্ষণিক ত্বরণ বলে।
অসম ত্বরণ কাকে বলে ?
যদি কোনো বস্তুর গতিকালে তার ত্বরণের মান বা দিক বা উভয়ই পরিবর্তিত হয় তবে সে ত্বরণকে অসম ত্বরণ বলে।
সুষম ত্বরণ কাকে বলে ?
কোনো বস্তুর বেগ যদি নির্দিষ্ঠ দিকে সবসময় একই হারে বাড়তে থাকে তাহলে সে ত্বরণকে সুষম ত্বরণ বা সমত্বরণ বলে ।
সমত্বরণ কাকে বলে ?
কোনো বস্তুর বেগ যদি নির্দিষ্ট দিকে সব সময় একই হারে বাড়তে থাকে, তাহলে সে ত্বরণকে সমত্বরণ বলে।
অসম ত্বরণ কাকে বলে ?
যদি কোনো বস্তুর গতিকালে তার ত্বরণের মান বা দিক বা উভয়ই পরিবর্তিত হয় তবে সে ত্বরণকে অসম ত্বরণ বলে।
মন্দন কাকে বলে ?
সময়ের সাথে সাথে কোনো বস্তুর বেগ হ্রাসের হারকে মন্দন বলা হয় ।
মন্দন কে ঋণাত্মক ত্বরণ বলা হয় এবং মন্দন একটি ভেক্টর রাশি ।
নির্দিষ্ট মন্দনে গতিশীল কোন বস্তুর প্রারম্ভিক বেগ u এবং t সময় পরে বেকমে বস্তুটির চূড়ান্ত বেগ v হলে,
অর্থাৎ, বস্তুটির মন্দন f = (u-v) / t
সুষম মন্দন কাকে বলে ?
কোনো বস্তুর বেগ যদি নির্দিষ্ট দিকে সবসময় একই হারে কমতে থাকে তাহলে সেই মন্দনকে সুষম মন্দন বা সমমন্দন বলে।
ত্বরণ ও মন্দনের পার্থক্য
| ত্বরণ | মন্দন |
|---|---|
| কোনো বস্তুর বেগ যদি ক্রমশ বাড়তে থাকে , তবে সেই বস্তুর বেগের পরিবর্তনের হারকে ত্বরণ বলা হয় | সময়ের সাথে সাথে কোনো বস্তুর বেগ হ্রাসের হারকে মন্দন বলা হয় |
| কোনো বস্তুর ত্বরণ হলে বস্তুটির বেগ বাড়তে থাকে | কোনো বস্তুর মন্দন হলে বস্তুটির বেগ কমতে থাকে |
| ত্বরণ ধনাত্মক রাশি | মন্দন ঋণাত্মক রাশি |
গতি, রৈখিক গতি, দ্বিমাত্রিক গতি এবং ত্রিমাত্রিক গতি কাকে বলে?
গতি
সময় পরিবর্তনের সাথে সাথে যখন কোনো বস্তু তার অবস্থান পরিবর্তন ঘটে, তখন তাকে বলা হয় গতিশীল বস্তু। আর বস্তুর এই অবস্থান পরিবর্তনের ঘটনাকে বলা হয় গতি।
দিক নির্দেশনা অনুসারে গতিকে তিনটি ভাগে ভাগ করা হয়। যেমন-
- রৈখিক গতি বা এক মাত্রিক : সময় পরিবর্তনের সাথে সাথে যখন কোনো বস্তুর অবস্থান একটি সরল রেখা বরাবর ঘটে, বা যদি কোনো বস্তুর গতি দিক পরিবর্তন না করে তবে তাকে রৈখিক গতি বলা হয়।
- সমতলীয় গতি দ্বিমাত্রিক গতি : সময় পরিবর্তনের সাথে সাথে যখন কোনো বস্তুর অবস্থান কোনো সমতলের উপর পরিবর্তিত হতে থাকে, তখন তাকে সমতলীয় গতি বা দ্বিমাত্রিক গতি বলা হয়।
- স্থানিক গতি বা ত্রিমাত্রিক গতি : সময় পরিবর্তনের সাথে সাথে যখন কোনো বস্তুর অবস্থান যে কো কোনো দিক পরিবর্তিত হতে থাকে, তখন সেই বস্তুর গতিকে ত্রিমাত্রিক গতি বা স্থানিক গতি বলা হয়।
VIDEO CONTENT (PART 2)
VIDEO CONTENT (PART 3)
![]()



